11272. Игра Ани

Маленькая девочка по имени Анна Спетринг любит играть в следующую игру. Она рисует круг на бумаге. Затем она рисует еще один и соединяет его с первым кругом линией. Затем она рисует еще один и соединяет его линией с одним из первых двух кругов. Она продолжает таким образом, пока не нарисует n кругов, и каждый из них соединится с одним из ранее нарисованных кругов. Ее круги никогда не пересекаются, и линии тоже никогда не пересекаются. Наконец, она нумерует круги от 1 до n в произвольном порядке.

Сколько разных картинок она может нарисовать, содержащих ровно n кругов? Два изображения различны, если на одном из них есть линия, соединяющая круг с номером i с кругом с номером j, а на другом нет.

Вход. Первая строка содержит количество тестов t. Каждый тест представляет собой строку, содержащую число n (0 < n ≤ 100).

Выход. Для каждого теста выведите строку, содержащую “Case #x:” за которой следует res, где res – остаток от деления ответа на 2000000011.

Пример входа	Пример выхода
3 1 2 3	Case #1: 1 Case #2: 1 Case #3: 3

РЕШЕНИЕ

графы – остовное дерево

Анализ алгоритма

В задаче требуется найти количество разных пронумерованных деревьев с n вершинами. Или то же самое что количество остовных деревьев в полном графе из n вершин (граф называется полным, если его две любые вершины соединены ребром).

Теорема. Существует взаимно однозначное соответствие между остовными деревьями для полного графа из n вершин и кодами Прюфера длины n – 2.

Лемма. Количество кодов Прюфера длины n – 2 равно n^n-2.

Значит количество рисунков, которое может изобразить Аня (число пронумерованных деревьев с n вершинами), равно n^n-2.

Пример

Для n = 4 имеем 16 деревьев. Под каждым деревом приведен его код Прюфера

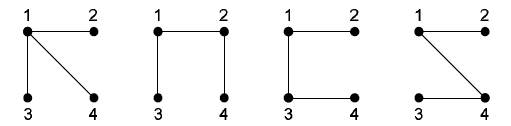
(1, 1) (1, 2) (1, 3) (1, 4)

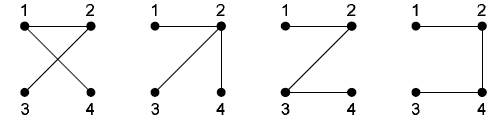
(2, 1) (2, 2) (2, 3) (2, 4)

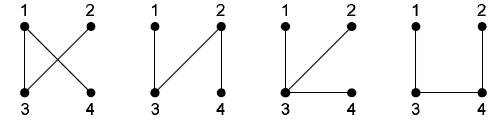
(3, 1) (3, 2) (3, 3) (3, 4)

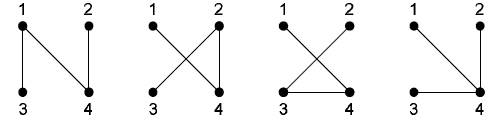
(4, 1) (4, 2) (4, 3) (4, 4)

Реализация алгоритма

Читаем количество тестов tests.

scanf("%d",&tests);

for(t = 1; t <= tests; t++)

{

Для каждого теста читаем значение n.

scanf("%d",&n);

Вычисляем и выводим результат n^n-2 (mod 2000000011) .

res = 1;

for(i = 0; i < n - 2; i++)

res = (res * n) % 2000000011;

printf("Case #%d: %lld\n",t,res);

}